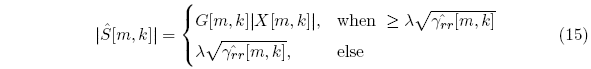Dereverberation using spectral subtraction removes reverberant speech energy by cancelling the energy of preceding phonemes in the current frame. This energy is only an estimation, and does not offer a perfect reconstruction, but does indeed remove the effect of reverberation.
Reverberation
Reverberation occurs when a microphone picks up multiple attenuated and delayed copies of a single signal. In speech communications applications, these copies are generated when sound reflects off surfaces in an environment. Attenuation occurs due to the surfaces absorbing some of the sound energy. Generally, these reflections are divided into two groups: Early Reflections and Late Reflections, as opposed to the Direct Sound.
The temporal masking properties of the human ear cause the early reflections to actually reinforce the direct sound, and thus we are mostly concerned with the effects of the late reflections. We perceive these signal reflections as adding color to the original speech sound, and introducing an echo. More specifically, reverberation tends to spread speech energy over time. This time-energy spreading has two distinct yet equally important effects. First, the energy in individual phonemes become more spread out in time. As a result, plosives have a markedly delayed onset and decay, and fricatives are smoothed. Secondly, preceding phonemes blur into the current ones. When a vowel precedes a consonant, this effect is most apparent. Both effects reduce speech intelligibility by reducing the information available for phonemic identification. It should be noted that these observations form the basis of the dereverbation technique discussed in this article.
Room Impulse Response Transfer Function
To deal with late reflections, not only must we understand how they affect speech, but also how they can be described. Late reflections are described by the Room Impulse Response transfer function, which is a statistical model of how reverberant energy fades over time, and is thought of as the transfer function of the room. As in [1-3], the room impulse response transfer function can be described as:
Where n is the discrete time index. The first term bN ͠ (0, σ) describes the room impulse response’s fine structure, and e-∆n is an exponentially decaying envelope. The most important parameters are the variance σ and the decay factor Δ. There is no explicit formula for σ, but Δ can be expressed as:
Where RT60 is the reverberation time of the room.
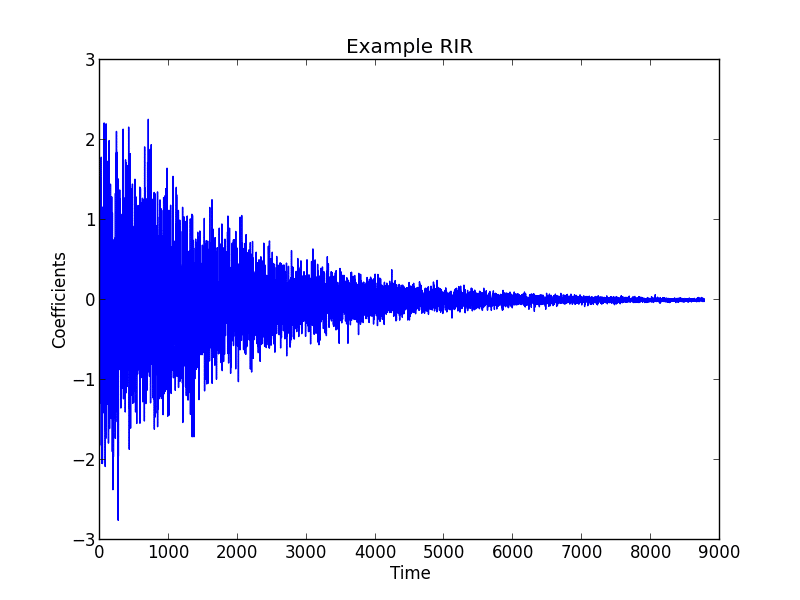
In reality, each frequency present will be absorbed and thus decay differently than others. Therefore, a more realistic model includes a frequency index. As an example of a room impulse response, see the figure below:
Figure 1: Example Room Impulse Response
If reverberation is thought of as the output of a linear system with the response expressed as the room transfer function, then dereverberation can theoretically be achieved by deconvolution. Unfortunately, it is almost always the case that this impulse response transfer function is unknown, and thus we can either attempt to estimate the room impulse response or find another means of removing reverberation. Here we will consider implementing a well known approach, Spectral Subtraction, for removing noise from speech.
Spectral Subtraction
Spectral subtraction for dereverberation was proposed by Lebart et al. in [2]. It works on the principle that the phonemic energy smearing can be approximated from knowledge of the preceding phonemes and the room’s reverberation time. This approximation can then be subtracted from the current energy, leaving us with an approximation of the clean speech signal. To arrive at this approximation, we let T be the lag at which the speech is considered stationary. Considering that sound energy decay is exponential, the reverberant energy’s power spectral density (psd) can be approximated as:
Where γxx is the psd of the available reverberant speech signal, n is the discrete time index, and k is the discrete frequency index. The astute reader will notice that we don’t generally have access to the room impulse response and thus we don’t know RT60 and so we cannot actually calculate Δ. However, we can estimate the reverberation time, and this will be discussed later. Given that we have estimated Δ, amplitude spectral subtraction is then performed as:
Where Ŝ is the short time Fourier transform of the estimated clean signal, X is the reverberant speech, and m is the frame index. Those skilled in the art will recognize the change in time reference, and notice that we will need to convert absolute lag T into frame lag T’, where T’ is expressed as:
Where fs is the sampling frequency and O is the percentage overlap in the STFT analysis frames. Then the reverberation psd can be re-expressed as:
While this is certainly instructive of the type of manipulations that we will need to do, this implementation can certainly be improved. The most obvious improvement would be to prevent the negative values possible from the subtraction in (4). Next, we could take additive noise into account. Finally, we may be able to incorporate more information to achieve better reverberant energy estimation. These improvements will be discussed later. For now, we will focus on estimating the reverberation time.
Estimating Reverberation Time
Ratnam et al [3,4] proposed a maximum likelihood approach to estimating the optimal reverberation time. In their approach, they let a[n] denote the exponential term in (3). For N observations, where N is the length of the mth frame, they assume a single decay rate is at work, so that they express the parameter a as:
With the variance σ as the second parameter, the likelihood function to maximize becomes:
To maximize this function, take the logarithm and differentiate it with respect to a:
Setting this result equal to zero and solving for a gives us the best estimate in the mean. Notice that they equation cannot be solved explicitly for a. Instead, it needs to be iteratively approximated. To do so in a computationally tractable manner, we quantize the possible values a ∈ [0, 1) can take such that we have a ∈ A = {a1, a2, …,aQ}. In [4], the authors recommend that Q ≤ 10, and for the most extreme environments set Q = 2. Then we can rewrite (8) as:
Then similarly to (9), we select the best estimate of a as:
From frame to frame, it is likely that this estimate of a will change. Therefore, we need a way to pick the best estimate of the per frame estimates. To do this, we note that sound decay cannot occur faster than following a period of silence. Since reverberation time is defined as sound decay in silence, we should be biased towards smaller values of a. As we accumulate these estimates, we can create a pmf and choose an estimate in the left tail with some error probability when the distribution is unimodal. Else, we select the median of the smallest distribution. When the distribution is highly multi-modal, we simply select the smallest mode.
Despite this extra computational burden, we can further simplify the implementation if we perform a recursive update on the arrival of the next sample. In other words, the computation of (10) can be performed as the reverberant samples are taken in by applying the following to term inside the second logarithm. We simply let β = a-2, and define:
Such that the recursive update is given by:
To speed up the calculation, pre-calculate all β terms, ln(aj) and ln(2π/n). Finally, ln(g[n]) can be calculated from a lookup table. This lookup can be handled in two ways, either quantize and threshold ln(g[n]) such that we will be assured the value can be found, or with no pre-manipulation when the requested value is not in the table, perform a linear interpolation between the two nearest values.
Improving Spectral Subtraction
Now that we have an online method for estimating the reverberation time, we will go back to considering how we can improve the spectral subtraction algorithm as a whole. First, we need to consider how to deal with negative values that may result when the reverberant energy is estimated to be larger than the signal magnitude. To start, we need to consider the subtraction as an application of a gain instead. We define the applied gain as:
To eliminate the possibility of negative values, we consider a “spectral floor” [1,2] such that when the modified signal is less than a threshold, we set it to that threshold. In other words, we define the subtracted spectrum as:
When λ = 0.1, it corresponds to an attenuation of 20 dB. Now that we have eliminated negative values, we need to consider how we can improve the reverberant psd estimator. Consider using a running average as below:
Where the weighting value η is computed as:
Simulation Results
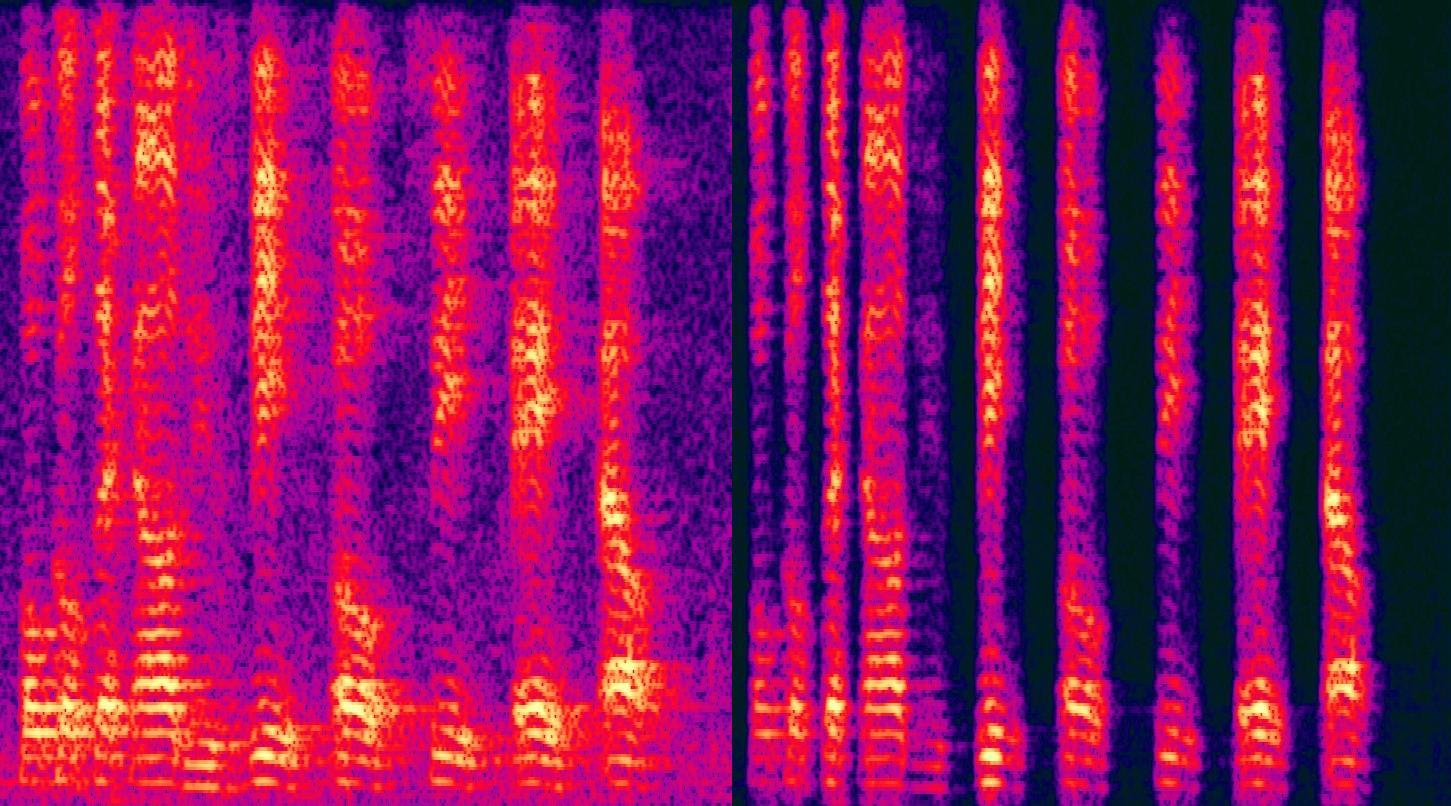
Speech was recorded by one of our engineers in our reverberant conference room. Obviously, we did not have the clean speech signal available, so any result is based on the strength of the adaptability of our algorithm. The before and after spectrograms (below) have been appended to clearly show the results of dereverberation processing.
VOCAL’s dereverberation algorithm removes reverberation while preserving the columns and comb structures of original speech
As you can see, our algorithm has greatly removed the reverberation as well as the noise. The speech comb structure is well preserved, and the speech columns have been made nearly exact. It should be noted that this result is obtained entirely with a single microphone, thereby eliminating the need for expensive hardware setups. In sum, spectral subtraction works to remove the reverberant speech energy by cancelling the energy of preceding phonemes in the current frame. This energy is only an estimation, and such does not offer a perfect reconstruction, but does indeed remove the effect of reverberation. As an online algorithm, spectral subtraction promises to be quick and effective. To improve the algorithm, aside from an optimal reverberation time estimator, we need an optimal estimate of T’, and an optimal attenuation factor λ.
References
[1] E. Habets, “Single and Multi-Microphone Speech Dereverberation using Spectral Enhancement, Ph.D. dissertation, Technische Universiteit Eindhoven, Eindhoven., 2007
[2] K. Lebart et al, “A New Method Based on Spectral Subtraction for Speech Dereverberation,” Acta Austica. Vol. 87, pp. 359-366, 2001.
[3] R. Ratnam et al, “Blind estimation of reverberation time”, Journal of the Acoustical Society of America. Vol. 114, No. 5, pp. 2877-2892, 2003.
[4] R. Ratnam et al, “Fast Algorithms for Blind Estimation of Reverberation Time”, IEEE Signal Processing Letters. Vol. 11, No. 6, pp. 537-540, 2004.